Editor's Note
The following transcripts accompany the main article, "Educational Technology at BBN," by Wallace Feurzeig, which appears in the January-March 2006 issue of IEEE Annals of the History of Computing. The material here was omitted from the main article because of space constraints.
Socratic System
The following excerpt from a student interaction with the Socratic System—concerning a medical application in this case—illustrates some of the system's instructional facilities. The system's capabilities for enabling the student to take the initative during the interaction, and for supporting history-sensitive responses to student inputs, were notable advances over current CAI systems in 1962.
The student's inputs are indented and capitalized to set them off from those of the system. The student's preliminary questions have been deleted. Here is the problem statement:
It is mid-December. Late this afternoon a patient was admitted to the hospital. He is a well-developed, well-nourished, 34-year-old coal miner. His wife reports that he has had "the grippe" for about 4 days. During the past 3 days she has given him fluids and aspirin every 6 hours with no sign of improvement. Today he suddenly became much worse. For the past 2 days he had complained of feeling very warm and of pain in his belly. This morning he had a severe shaking chill that was so bad his teeth rattled.
[Deleted: Student's initial requests for vital signs and other physical exam items, and for some lab tests.]
Before proceeding with the examination, it might be instructive to pause and consider the diagnostic implications of the information at hand. Perhaps you think it too early to arrive at a definitive conclusion. On the other hand, you may be prepared to make the diagnosis now. Are you?
NO.
Fine. Nevertheless, we've got a fair amount of information—at least enough to raise some, perhaps several, diagnostic possibilities. Have you any in mind?
YES.
Name one.
PNEUMOCOCCAL PNEUMONIA.
Good. The general signs of a pneumonic process are present. Of course, you haven't isolated the bug. Do you think the belly pain and flank pain reinforce the case for pneumococcal pneumonia?
NO.
Right. Though the white count is consistent, isn't it?
YES.
I think so too, but a later reading is indicated to confirm this finding. We've considered one possibility. Do you have another diagnosis in mind?
NO.
In that case, I'd like to talk about pulmonary infarction. What I like about that diagnosis is the presence of high fever, rusty sputum, and shaking chills. I don't like the dyspnea, pleural pain, and signs of consolidation—do you agree?
NO.
You're quite correct. I was just trying to see whether you were alert—and you were. Now let's see how the patient is today. Begin the physical when you're ready.
[Deleted: Student requests for vital signs and other physical exam items.]
PNEUMOCOCCAL PNEUMONIA.
Yes. I remember you liked this diagnosis before. Are you absolutely sure?
NO.
What would help you nail down the diagnosis?
EVIDENCE FROM SPUTUM SMEAR AND CULTURE.
Good. Anything else?
EVIDENCE FROM X-RAY FINDINGS.
Good. X-ray shows area of consolidation at right lower lobe, consistent with a pneumonic process. Lab reports gram positive organisms in the sputum smear and the presence of pneumococci in the culture. Had you thought to rule out things like appendicitis and acute pyelonephritis?
YES
Apparently you weren't thrown off by the referred abdominal pain. In any case, you've made the correct diagnosis.
In this example the student was fairly insightful. Some students made ill-informed diagnostic guesses. When the evidence for their diagnoses was absent or weak, the program demanded additional confirmatory findings.
Buggy
The following excerpt illustrates the use of the Buggy computer game by a team of teachers trying to diagnose students' conceptual errors ("bugs") on arithmetic problems. It shows the system's capability for evaluating whether subtraction problems input by the users correctly instantiate the problem bug presented by the system.
The teachers' inputs are preceded by vertical lines on the left.
I HAVE CHOSEN A BUG. HERE IS AN EXAMPLE OF THE BUG.
17
+5
13
NOW YOU CAN GIVE ME PROBLEMS TO DETERMINE THE BUG.
| 18 43
| +6 +79
15 23
| Got the bug!
HERE IS A PROBLEM TO TEST YOUR THEORY ABOUT THE BUG. WHAT IS:
21
+39
| 51
THAT'S NOT THE BUG I HAVE. USING MY BUG:
21
+39
| 15
TRY GIVING ME SOME MORE EXAMPLES.
| 51 99 68
|+1707 +99 +9
21 36 23
| Got the bug!
PLEASE DESCRIBE THE BUG YOU THINK I HAVE.
| The student is adding all the digits together.
HERE ARE SOME PROBLEMS TO TEST YOUR THEORY. WHAT IS:
33 1091 8 28 90
+99 +60 +34 +70 +6
24 17 15 17 15
VERY GOOD. MY DESCRIPTION OF THE BUG IS: THE STUDENT ALWAYS SUMS UP ALL THE DIGITS WITH NO REGARD TO COLUMNS.
Function Machines
Function Machines is a visual programming environment designed to support the learning and teaching of mathematics. This excerpt illustrates a Function Machines activity in a pre-algebra sequence called Guess My Rule. The Put In and Get Out machines are as described in the main article, "Educational Technology at BBN." The Mystery machine, however, is new. It has concealed inside it two calculation machines: + (an addition machine), and * (a multiplication machine).
The activity proceeds as follows. Students are organized into groups of five. Each group has a computer with the Guess My Rule program installed. Group A creates two calculation machines and conceals them inside the Mystery machine in Group B's computer. The task of Group B is to run Group A's Guess My Rule program with a variety of inputs, and to determine from the resulting outputs, which two calculation machines are inside the Mystery machine. At the same time, Group B makes a pair of calculation machines and conceals them inside another Mystery machine, that of Group A, and the kids in Group A try to determine what's inside their Mystery machine. This "guessing game" exercises students' thinking about arithmetic operations. At the same time, kids find this an engaging and "fun" activity. Figure 1 shows a session of Guess My Rule in progress.
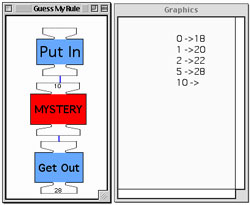
Figure 1. Guess My Rule activity in a fifth-grade pre-algebra sequence.
The display shows that inputs 0, 1, 2, and 5 produce outputs of 18, 20, 22, and 28, respectively. The current input, 10, is about to be run by the Mystery machine. The students try to guess what output it will generate.
Figure 2 shows the inner contents of the Mystery machine used in the above session—the two machines +9 and *2. It is not a trivial task for fifth-graders to find this or other possible solutions. (For example, instead of the machines +9 and then *2, an equivalent Mystery machine is *2 and then +18.)
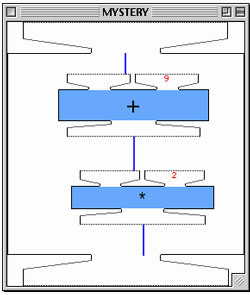
Figure 2. Inner contents of the Mystery machine used for the Guess My Rule activity.
After determining what output would be produced by a given input, the kids are given a challenging new task—to answer the opposite question: What number must be input to produce a specified output? For example, using the given +2 and *5 machines, what number must be Put In to Get Out 100? The problem is presented in the left window of Figure 3.
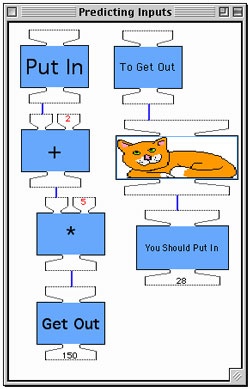

Figure 3. Using the left window, fifth-graders use trial and error to predict what numbers should be entered to determine what input will produce an output of 100, shown in the window on the right.
Understandably, this seems to the kids a much more difficult problem. They are encouraged to approach the task by trial and error. The display screen on the right shows the results of a trial-and-error sequence aimed at finding what input yields an output of 100. The input 10 yields 60, so perhaps a larger input is needed. An input of 20 yields 110. So perhaps some input between 10 and 20 is called for—15 yields 85; 17 yields 95, and then: "Hooray! 18 works! It only took five trials."
Using the same pair of machines with other output targets, kids attempt to determine the correct inputs in as few trials as possible. They are delighted when they can zoom in on the answer in three or four trials and sometimes even two!
At this point, the two new machines in the left window, To Get Out and You Should Put In, are introduced. The inputs and outputs printed by these machines are shown on the right half of the display screen. Just after the printout on the left was produced, showing that an input of 18 produces an output of 100, the two new machines are run. An input of 100, the target output in the previous problem, is given to the To Get Out machine. This input is piped to the You Should Put In machine, which produces the printout of 18 shown on the display. Somehow, using this pair of machines, all one had to do was give it the desired output and it produced the corresponding input—and in just a single trial! Also, as the subsequent printout from this machine shows, it confirms what was shown before: that obtaining an output of 60 requires an input of 10. And it could be used to confirm the other pairs also: that an output of 110 calls for an input of 20, and so on. Instead, however, it is used to assert a new claim, that to get an output of 150 requires an input of 28. The last printout on the left of the display, generated by running the four machines on the left, confirms this: An input of 28 indeed yields an output of 150.
The problem for the students is: How does the You Should Put In machine know, right from the start, what input one needs to put in to get a desired output? What does the Magic machine (the machine covered by the cat) do? The kids are not expected to fathom the answer. Instead, they are shown the inner contents of the Magic machine, seen in Figure 4.
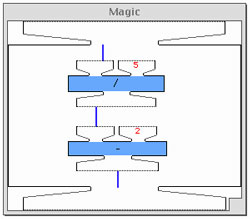
Figure 4. Inner contents of the Magic machine.
As the figure illustrates, the solution to the problem is to do the inverse computations in the opposite order. (This is the same algorithm used for turtle path reversal in Logo.) The original computation sequence was: Put in a number (say N), add 2 to it, multiply the result by 5, and get out the answer. To undo this sequence, one computes operations in the reverse order from the original sequence, replacing the original operations with their inverses, as follows. Put in the desired answer, divide it by 5, subtract 2 from the result and get out N. This is essentially the algorithm for solving linear equations in algebra, whose sense and purpose fifth-graders can understand in this context.