Fermat Meets SWAC: Vandiver, the Lehmers, Computers and Number Theory

Editor's Note

The following appendix accompanies the main article, "Fermat Meets SWAC: Vandiver, the Lehmers, Computers, and Number Theory," by Leo Corry, which appears in the January-March 2008 issue of the IEEE Annals of the History of Computing. The material here was omitted from the main article because of space constraints.

Appendix

Ernst E. Kummer's results are interestingly related to a discussion on the problem held in 1847 at the Paris Academy among prominent mathematicians that included Gabriel Lamé as well as Augustin Louis Cauchy (1789–1857) and Joseph Liouville (1809–1882). A possible proof of the theorem was suggested, based on representing a sum of integers as a product of certain complex numbers, as follows:

 

x^p + y^p= (x + y)(x + ry)(x + r²y) … (x + r^p-1y)  (*)

 

Here p is an odd prime number, and r is a complex number called a primitive p^throot of unity, namely, a number that satisfies the condition: r^p= 1 and r ¹ 1. A domain of complex numbers generated by a p^throot of unity is called a "cyclotomic field," k(z_p). The strategy was to start from (*) and to apply the method of "infinite descent" in order to lead to a contradiction that would prove the theorem. Now, a fundamental property of the integers is that when one factorizes an integer number (or an expression involving integers like the left-hand side of (*)) into a product of primes, this can be done in an essentially unique way. An implicit assumption behind this intended proof was that this condition of uniqueness is satisfied also when the numbers in the right-hand side of (*) are "prime integers" (in a well-defined sense) within k(z_p).

Several years prior to that, however, as part of his research on higher reciprocity, Kummer had investigated the behavior of cyclotomic fields, and he knew well that this assumption is not generally valid for such domains. On hearing about their intended proof, he wrote to Liouville, informing him that in 1844 he had already published a counterexample to that assumption. He also wrote that his new theory of "ideal complex numbers" restored a somewhat different kind of unique prime factorization into these fields. While working on his theory, Kummer came up with the idea of the regular primes.

The basic definition of a regular prime uses the concept of "class number" h_p of a cyclotomic field k(z_p). h_p provides a "measure" of the failure of unique factorization of integers in that domain. Thus, the prime number p is said to be regular whenever p does not divide h_p. This basic definition, however, does not provide an easily implementable procedure for identifying a given prime as regular or irregular. Kummer soon found a more operational criterion for allowing this identification, based on the use of so-called Bernoulli numbers.

The Bernoulli numbers appeared for the first time in 1713 in the pioneering work of Jakob Bernoulli on probabilities, and thereafter in several other contexts. Leonhard Euler, for instance, realized that they appear as coefficients B_n of the following Taylor expansion:

 

 

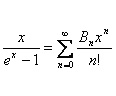
He was also the first to calculate actual values of the coefficients. There are also several, well-known recursion formulas to calculate them. Given that for all odd indexes n greater than 1, B_n = 0, I followed in this article a simplifying convention adopted by Harry Schultz Vandiver and Dick and Emma Lehmer, namely, to consider only even indexes. In these terns, the first few values of B_n are:

 

B₁= 1/6

B₂= –1/30

B₃= 1/42

B₄= –1/30

B₅= 5/66

B₆= –691/273

 

Kummer showed that a prime p is regular iff it does not divide the numerators of any of the Bernoulli numbers B₀, B₂, … , B_(p-3)/2. Already in the lower cases one sees that B₆= –691/2,730, which shows directly that 691 is an irregular prime.

As a measure of Kummer's willingness to undertake arduous computations with individual cases it is worth noticing that the lowest case for which unique factorization fails in the cyclotomic fields k(z_p), is p= 23.  Kummer obviously had made extensive and difficult calculations with numbers of all kinds before coming to realize that a case like this one may arise at all. Also in the case of the irregular primes, Kummer made extensive calculations, and the importance of some of these became clear only much later on. Thus, for instance, for all irregular primes under 157, he found that the class number was divisible by p only, whereas for p = 157, the class number is divisible by 157² and then again not by 157³.

Kummer's three criteria for the validity of the theorem for irregular primes involve the class number h_p as well as several divisibility relations vis-à-vis certain Bernoulli numbers. One case to which they do not apply is p= 157.